- トップページ
- 想像を超えるアイデアソース
- 第三十四回 想像を超える「比率」
サプライズを創出し続ける人々の
想像を超えるアイデアソースをご紹介します。
2018年6月1日
第1GF開発チーム 山田 康雄さんのアイデアソース
第三十四回
想像を超える「比率」
偶然か、必然か
皆さんは黄金比という言葉をご存知でしょうか。外中比、黄金分割などいろいろな呼び方がありますが、近似値1：1.618、この比率を黄金比といいます。この比率の名前が使われ始めたのは1800年代からですが、比率自体は紀元前300年頃から使われていたようです。この比率がおもしろいのは、幾何学や芸術作品、オウムガイの殻の形や音楽、文学、株価推移まで、この比率で語ることができる点です（身近な例でいうと名刺の縦と横の比率もそうです）。
定義は、次のようになります。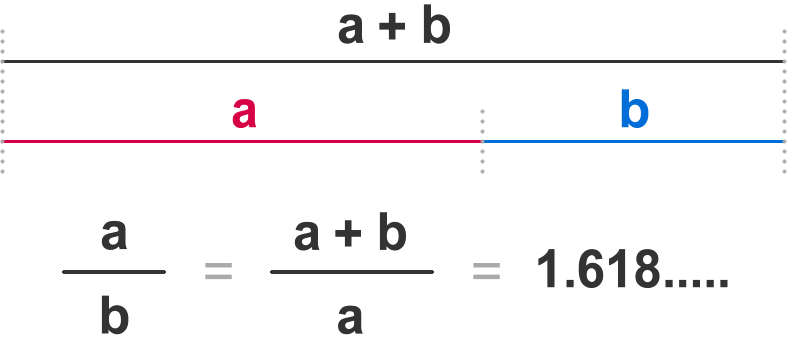
この黄金比が美しいと言われる理由は2つあります。1つは、自然界に多く存在しバランスがよく安定している点、もう1つは数学的にとても美しく表現できる点です。幾何学的には五角形の一辺と対角線の比、五茫星の二等辺三角形の短辺と長辺の比、美術でいえば、S.ダリが描いた「最後の晩餐の秘蹟」の背後に描かれている巨大な正12面体も黄金比であらわされています。ピラミッドの側面の三角形の高さと底辺の半分の比もそうですし、数式的なところではX?＝X+1できれいな１の連分数になり、フィボナッチ数列も黄金比であらわすことができます（連続するフィボナッチ数は黄金比に収束する）。
このように本書にはさまざまな例が書かれていて、とても楽しく数学を学ぶことができる内容になっています。数の成り立ちやπやφについても書かれていますし、ピタゴラスやユークリッドが頻繁に登場し、その言葉や教訓も印象的でした。個人的にはピタゴラス（学派）が無理数の存在に気づいたエピソードが面白いと思いました。
大昔の人びとが美術や建築に、この比率を意図して使っていたのか偶然なのかはわりませんが、世の中には不思議で未知なことが多々あります。私はこの本を読んで、その不思議に触れてとても面白く感動しました。分野にとらわれず、いろいろな本（数学読本など）を読んで知識を深めたいとも思いました。皆さんも機会があれば、普段読まない分野の本を読んでみてはいかがでしょうか。思わぬ発見、感動があるかもしれません。
定義は、次のようになります。
この黄金比が美しいと言われる理由は2つあります。1つは、自然界に多く存在しバランスがよく安定している点、もう1つは数学的にとても美しく表現できる点です。幾何学的には五角形の一辺と対角線の比、五茫星の二等辺三角形の短辺と長辺の比、美術でいえば、S.ダリが描いた「最後の晩餐の秘蹟」の背後に描かれている巨大な正12面体も黄金比であらわされています。ピラミッドの側面の三角形の高さと底辺の半分の比もそうですし、数式的なところではX?＝X+1できれいな１の連分数になり、フィボナッチ数列も黄金比であらわすことができます（連続するフィボナッチ数は黄金比に収束する）。
このように本書にはさまざまな例が書かれていて、とても楽しく数学を学ぶことができる内容になっています。数の成り立ちやπやφについても書かれていますし、ピタゴラスやユークリッドが頻繁に登場し、その言葉や教訓も印象的でした。個人的にはピタゴラス（学派）が無理数の存在に気づいたエピソードが面白いと思いました。
大昔の人びとが美術や建築に、この比率を意図して使っていたのか偶然なのかはわりませんが、世の中には不思議で未知なことが多々あります。私はこの本を読んで、その不思議に触れてとても面白く感動しました。分野にとらわれず、いろいろな本（数学読本など）を読んで知識を深めたいとも思いました。皆さんも機会があれば、普段読まない分野の本を読んでみてはいかがでしょうか。思わぬ発見、感動があるかもしれません。
黄金比はすべてを美しくするか？
- 著
- マリオ・リヴィオ
- 訳
- 斉藤 隆央
- 出版
- 早川書房
- 価格
- 840円＋税
過去に紹介されたアイデアソース
当サイトは、Amazon.co.jpを宣伝しリンクすることによってサイトが紹介料を獲得できる手段を提供することを目的に設定されたアフィリエイト宣伝プログラムである、Amazonアソシエイト・プログラムの参加者です。